Presidential Prediction

Published

November 2, 2024

Disclamer: i collected all the data and ran all this models in like 2 hours. I did not put much effort into this, its not very good. Just for fun. Might add ridge lasso later but lazy.

3 types of models on here (use table of contents to access or scroll down)

  1. Electoral College Prediction Models
  2. Winner/Loser Prediction Models
  3. My own gut based prediction (with map!)


Electoral Votes Predictions

I create 3 different predictions for the 2024 election for each model.

  • Most Likely Scenario: polls say harris leads by 1.2% (according to 538 aggregator, seems to be most accurate)

  • Moderately Likely Scenario: polls say harris leads by 2% (the economist aggregator rounded up)

  • Unlikely Scenario: If polls say harris leads by 3% (a few polls say this, but unlikely to be true).


2 Best Models (by recent performance)

Random Forest Model (5 Variables Bootstrap Sampled) With Height Excluded:

Most Likely: If harris leads 1.2% in polls: Harris 266.97, Trump 271.03

  • If harris leads 2% in polls: Harris 269.24, Trump 268.76

  • If harris leads 3% in polls (unlikely): Harris 297, Trump 241

Past Performance (5 out of last 6 elections correct winner)

2020 2016 2012 2008 2004 2000
Model (Incumbent) 250.5 264.2 317.4 188.6 285.1 272.9
Correct Winner? Yes Yes Yes Yes Yes No
Actual (Incumbent) 232 227 332 173 286 266
Incumbent Trump Clinton Obama McCain Bush Gore

% of Variance Explained in \(Y\) (Electoral Votes Received by Incumbent): 42.15%



Random Forest Model (5 Variables Bootstrap Sampled) with Height Included:

Most Likely: If harris leads 1.2% in polls: Harris 267.88, Trump 270.12

  • If harris leads 2% in polls: Harris 271.96, Trump 266.04

  • If harris leads 3% in polls (unlikely): Harris 296.45, Trump 241.5

Past performance (5 out of last 6 elections correct winner)

2020 2016 2012 2008 2004 2000
Model (Incumbent) 253.5 267.6 313.7 191.2 272.7 276.2
Correct Winner? Yes Yes Yes Yes Yes No
Actual (Incumbent) 232 227 332 173 286 266
Incumbent Trump Clinton Obama McCain Bush Gore

% of Variance Explained in \(Y\) (Electoral Votes Received by Incumbent): 37.64%


Other Models

Random Forest (20 Variables Boostrap Sampled) with Height:

  • If harris leads 1.2% in polls: Harris 229.14 Electoral votes, Trump 308.86

  • If Harris leads 2% in polls: Harris 232.33 Electoral Votes, Trump 305.67

  • If Harris leads by 3% in polls (unlikely): Harris 290.29 Electoral Votes, Trump 247.7

Past performance (4 out of last 6 elections correct winner)

2020 2016 2012 2008 2004 2000
Model (Incumbent) 237.6 278.9 300.2 186.5 259 261.4
Correct Winner? Yes No Yes Yes No Yes
Actual (Incumbent) 232 227 332 173 286 266
Incumbent Trump Clinton Obama McCain Bush Gore

% of Variance Explained in \(Y\) (Electoral Votes Recieved by Incumbent): 56.94%


Bagging Model with Height Excluded:

  • If harris leads 1.2% in polls: 229.66 Harris, 308.34 Trump

  • If harris leads 2% in polls: 235.41 Harris, 302.59 Trump

  • If harris leads by 3% in polls (unlikely): 307 Harris, 231 Trump

Past Performance (4 out of last 6 elections correct winner)

2020 2016 2012 2008 2004 2000
Model (Incumbent) 225 294.7 302.8 190.4 263.2 253.7
Correct Winner? Yes No Yes Yes No Yes
Actual (Incumbent) 232 227 332 173 286 266
Incumbent Trump Clinton Obama McCain Bush Gore

% of Variance Explained in \(Y\) (Electoral Votes Received by Incumbent): 54.12%


Random Forest (19 Variables Bootstrap Sampled) With Height Excluded:

  • If harris leads 1.2% in polls: 227.07 Harris, 310.93 Trump

  • If harris leads 2% in polls: 229.9 Harris, 308.1 Trump

  • If harris leads 3% in polls (unlikely): 290.72 Harris, 247.28 Harris

Past Performance (4 out of last 6 elections correct winner)

2020 2016 2012 2008 2004 2000
Model (Incumbent) 227.5 281.8 306.2 184.2 264.3 258.2
Correct Winner? Yes No Yes Yes No Yes
Actual (Incumbent) 232 227 332 173 286 266
Incumbent Trump Clinton Obama McCain Bush Gore

% of Variance Explained in \(Y\) (Electoral Votes Received by Incumbent): 56.42%


Bagging With Height:

  • If harris leads 1.2% in polls: Harris 215.74, Trump 332.26

  • If harris leads 2% in polls: Harris 221.1, Trump 316.9

  • If harris leads 3% in polls (unlikely): Harris 293.18, Trump 244.82

Past Peformance (4 out of last 6 elections correct winner)

2020 2016 2012 2008 2004 2000
Model (Incumbent) 230.7 292.4 296.2 185.2 254.4 259.4
Correct Winner? Yes No Yes Yes No Yes
Actual (Incumbent) 232 227 332 173 286 266
Incumbent Trump Clinton Obama McCain Bush Gore

% of Variance Explained in \(Y\) (Electoral Votes Received by Incumbent): 55.92%


Win/Lose Probability Predictions

Note: Every model in this section correctly predicts the election winners of the last 7 elections.

Aggregate: All believe Trump will win if Harris leads by only 1.2% or 2% in polls.


Naive Bayes Without Height:

  • Most Likely - If harris leads 1.2% in polls: Trump wins

  • Moderately Likely - If harris leads 2% in polls: Trump wins

  • Unlikely - If harris leads 3% in polls: Harris wins

Past performance (6/6 for the last 6 elections)

2020 2016 2012 2008 2004 2000
Model (Incumbent Result) Lost Lost Won Lost Won Lost
Correct Winner? Yes Yes Yes Yes Yes Yes
Actual (Incumbent) Lost Lost Won Lost Won Lost
Incumbent Trump Clinton Obama McCain Bush Gore

Error rate over last 22 elections: NA (too lazy to calculate)


Bagging Model Without Height:

  • Most Likely - If harris leads 1.2% in polls: Trump Wins

  • Moderately Likely - If harris leads 2% in polls: Trump wins

  • Unlikely - If harris leads 3% in polls: Trump wins

Past performance (6/6 for the last 6 elections)

2020 2016 2012 2008 2004 2000
Model (Incumbent Result) Lost Lost Won Lost Won Lost
Correct Winner? Yes Yes Yes Yes Yes Yes
Actual (Incumbent) Lost Lost Won Lost Won Lost
Incumbent Trump Clinton Obama McCain Bush Gore

Error rate over last 22 elections: 22.73%


Random Forest (5 variables bootstrapped) Without Height:

  • Most Likely - If harris leads 1.2% in polls: Trump Wins

  • Moderately Likely - If harris leads 2% in polls: Trump wins

  • Unlikely - If harris leads 3% in polls: Trump wins

Past performance (6/6 for the last 6 elections)

2020 2016 2012 2008 2004 2000
Model (Incumbent Result) Lost Lost Won Lost Won Lost
Correct Winner? Yes Yes Yes Yes Yes Yes
Actual (Incumbent) Lost Lost Won Lost Won Lost
Incumbent Trump Clinton Obama McCain Bush Gore

Error rate over last 22 elections: 27.27%


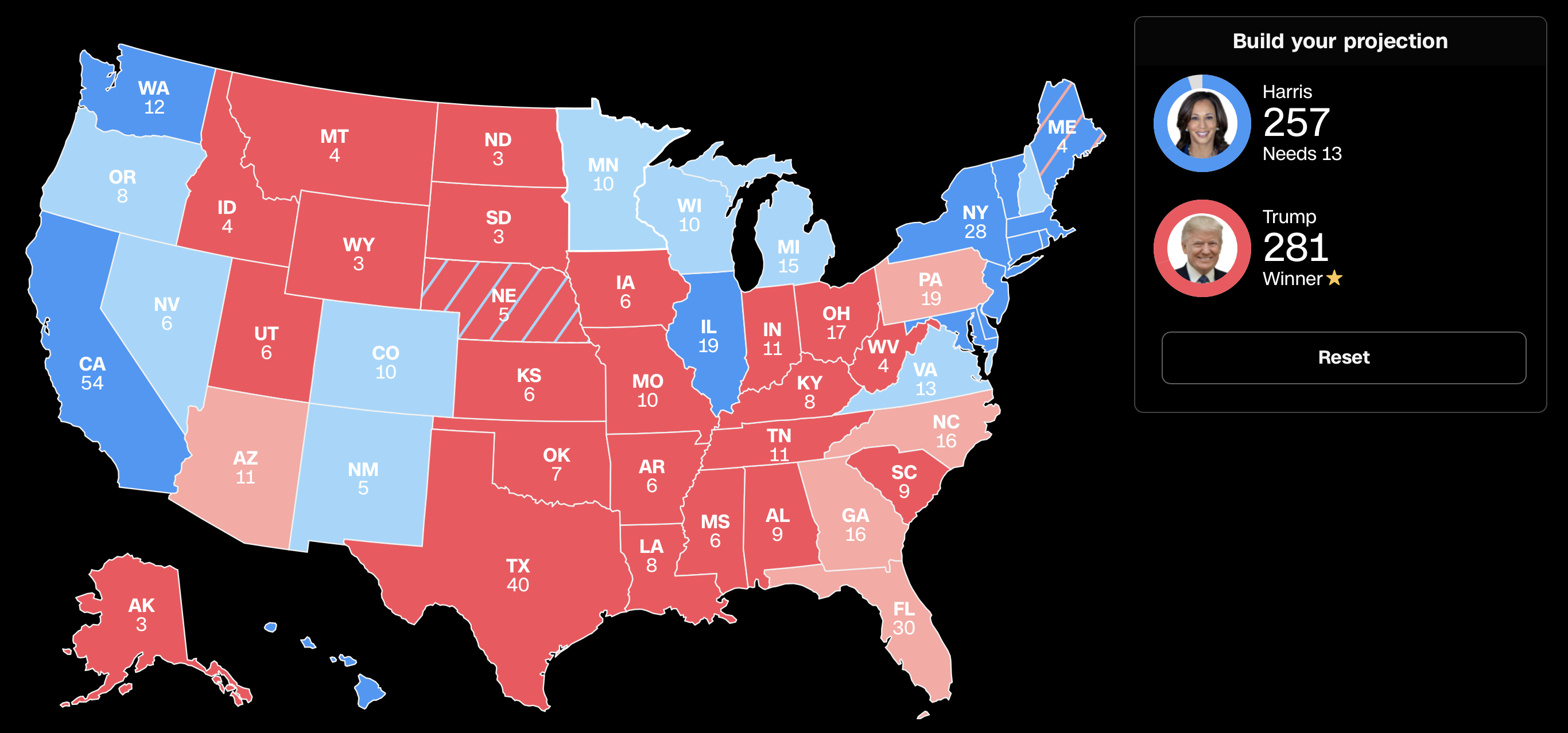
My Personal (Gut-Based) Predictions

My Personal Map


The Data in My Models

I used the following variables (that I gathered in like one hour). I did not check data quality, could be terrible.

  1. Year
  2. Incumbent Party
  3. Reelection (is on of the candidates the current president)
  4. Terms current party is in office continuously
  5. Poll margin (incumbent party candidate- challenger)
  6. Real GDP Growth in election year
  7. Unemployment rate in election rate
  8. Inflation rate in election year
  9. Incumbent party president average approval rating (gallup)
  10. Incumbent party president highest approval rating (gallup)
  11. Incumbent party president lowest approval rating (gallup)
  12. Recession occurred in the past 4 years?
  13. House net change in seats (of incumbent party) during the midterm election 2 years before the election
  14. House net change in seats (of incumbent party) during the election 4 years ago
  15. House change in seats (of incumbent party) for both midterm and 4 year ago election combined.
  16. Incumbent party faced a primary challenge? (challenge defined as winner of primary recieved less than 60% of votes. I classify harris is no-primary challenge).
  17. S&P 500 Returns in election year
  18. Midterm house elections from 2 years ago, incumbent party’s vote share overall (entire country)
  19. % Change in Jobs from last election to this election (a full presidential term)
  20. Height of the candidates (incumbent - challenger)
  21. Real estate returns in election year
  22. Treasury 10-year bond returns in election year.
  23. Does incumbent party have majority in House?
  24. Does incumbent party have majority in Senate?
  25. How many workers were furloughed as a result of a government shutdown during the current administration?
  26. Did any of the 15 largest tax rises in history occur during the current administration? If so, how much was the tax rise (% wise)
  27. Did any of the 15 largest tax breaks in history occur during the current administration? If so, how much was the tax break (% wise)
  28. The last two data points but net.


Start with the data analysis.

Load packages, clean data

library(tidyverse)
library(randomForest)
setwd("/Users/kevinli/Documents/GitHub/kevinli03.github.io/election/us2024")
data <- read_csv("data.csv")

clean data

dta <- data[-c(1:3),] # get rid of first 3 row
dta <- dta %>%
  select(-c(Incumbent, Challenger))

Electoral College (R Code)

Models with Height

Bagging:

set.seed(32435)
bagging <- randomForest(Pct_incumb ~ .,
                        ntree = 501,
                        nodesize = 1,
                        data = dta,
                        na.action = na.omit,
                        mtry = 28,
                        importance = TRUE)
bagging

Call:
 randomForest(formula = Pct_incumb ~ ., data = dta, ntree = 501,      nodesize = 1, mtry = 28, importance = TRUE, na.action = na.omit) 
               Type of random forest: regression
                     Number of trees: 501
No. of variables tried at each split: 28

          Mean of squared residuals: 0.03047664
                    % Var explained: 55.92
set.seed(32435)
#prediction
data2024 <- data[1:9,]
data2024 <- data2024[,-c(2,3,4)]


set.seed(32435)
bagging_pred <- predict(bagging, newdata = data2024)
bagging_pred * 538
       1        2        3        4        5        6        7        8 
215.7469 221.1062 293.1835 230.7959 292.4063 296.2063 185.2304 254.4689 
       9 
259.4328


Random Forest (5 variables boostrap Sampled):

set.seed(32435)
forest <- randomForest(Pct_incumb ~ .,
                        ntree = 501,
                        nodesize = 1,
                        data = dta,
                        na.action = na.omit,
                        mtry = 5,
                        importance = TRUE)
forest

Call:
 randomForest(formula = Pct_incumb ~ ., data = dta, ntree = 501,      nodesize = 1, mtry = 5, importance = TRUE, na.action = na.omit) 
               Type of random forest: regression
                     Number of trees: 501
No. of variables tried at each split: 5

          Mean of squared residuals: 0.043118
                    % Var explained: 37.64
# predictions
set.seed(32435)
forest_pred <- predict(forest, newdata = data2024)
forest_pred * 538
       1        2        3        4        5        6        7        8 
267.8893 271.9680 296.4508 253.5039 267.6710 313.7579 191.2754 272.7308 
       9 
276.2091


Random Forest (20 Variables boostrap sampled)

set.seed(32435)
forest <- randomForest(Pct_incumb ~ .,
                        ntree = 501,
                        nodesize = 1,
                        data = dta,
                        na.action = na.omit,
                        mtry = 20,
                        importance = TRUE)
forest

Call:
 randomForest(formula = Pct_incumb ~ ., data = dta, ntree = 501,      nodesize = 1, mtry = 20, importance = TRUE, na.action = na.omit) 
               Type of random forest: regression
                     Number of trees: 501
No. of variables tried at each split: 20

          Mean of squared residuals: 0.02977701
                    % Var explained: 56.94
set.seed(32435)
forest_pred <- predict(forest, newdata = data2024)
forest_pred * 538
       1        2        3        4        5        6        7        8 
229.1486 232.3351 290.2950 237.6001 278.9861 300.2055 186.5987 259.0048 
       9 
261.4613

Importance

varImpPlot(bagging, type = 2)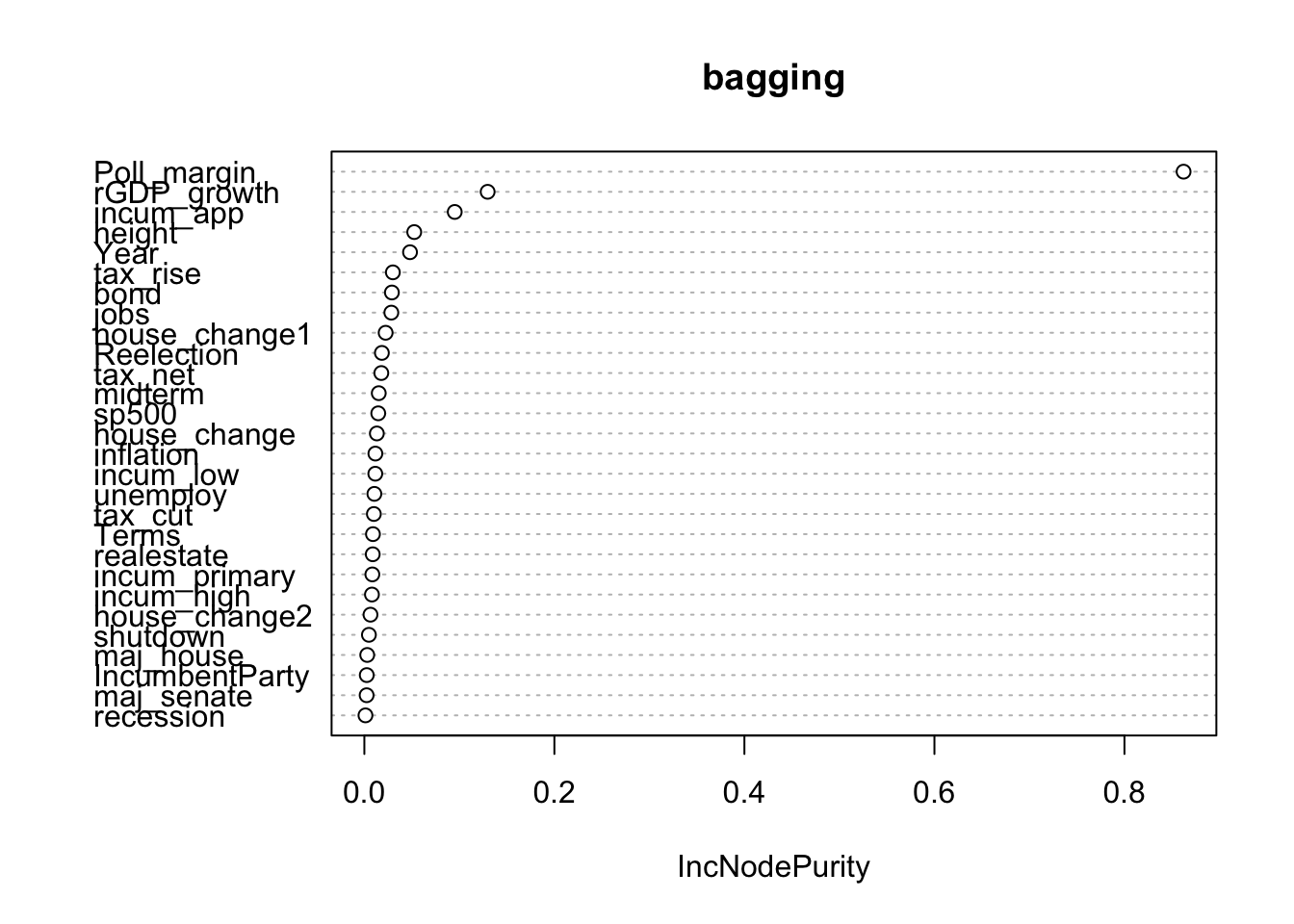

varImpPlot(forest, type = 2)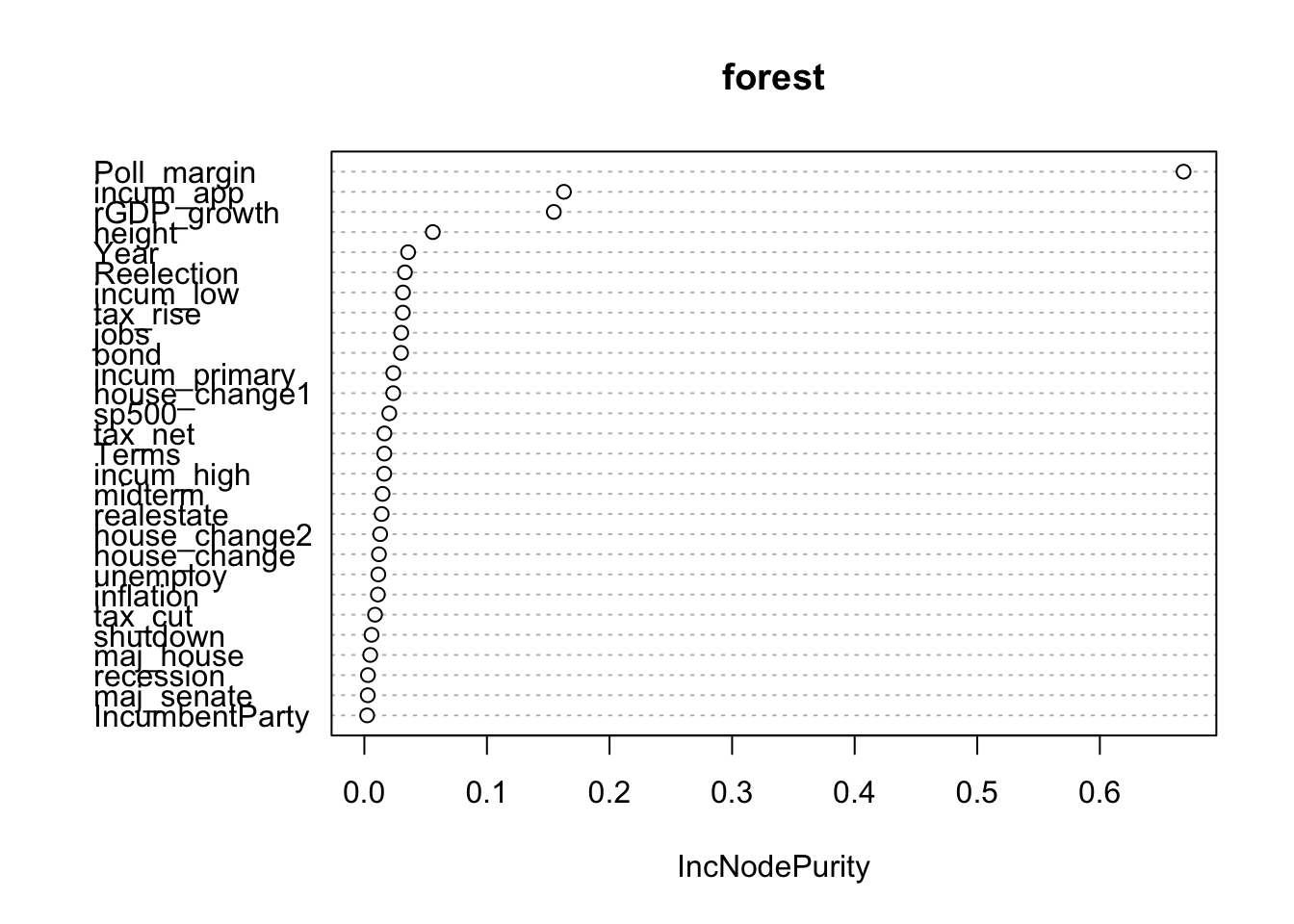


Models without Height

dta_noheight <- dta %>%
  select(-height)
data2024_noheight <- data2024 %>%
  select(-height)


bagging

set.seed(32435)
bagging1 <- randomForest(Pct_incumb ~ .,
                        ntree = 501,
                        nodesize = 1,
                        data = dta_noheight,
                        na.action = na.omit,
                        mtry = 27,
                        importance = TRUE)
bagging1

Call:
 randomForest(formula = Pct_incumb ~ ., data = dta_noheight, ntree = 501,      nodesize = 1, mtry = 27, importance = TRUE, na.action = na.omit) 
               Type of random forest: regression
                     Number of trees: 501
No. of variables tried at each split: 27

          Mean of squared residuals: 0.03172727
                    % Var explained: 54.12
set.seed(32435)
bagging_pred1 <- predict(bagging1, newdata = data2024_noheight)
bagging_pred1 * 538
       1        2        3        4        5        6        7        8 
229.6651 235.4156 307.0048 225.0212 294.7422 302.8635 190.4628 263.2217 
       9 
253.7652


Random forst (19 variables boostrap sampled)

set.seed(32435)
forest1 <- randomForest(Pct_incumb ~ .,
                        ntree = 501,
                        nodesize = 1,
                        data = dta_noheight,
                        na.action = na.omit,
                        mtry = 19,
                        importance = TRUE)
forest1

Call:
 randomForest(formula = Pct_incumb ~ ., data = dta_noheight, ntree = 501,      nodesize = 1, mtry = 19, importance = TRUE, na.action = na.omit) 
               Type of random forest: regression
                     Number of trees: 501
No. of variables tried at each split: 19

          Mean of squared residuals: 0.03013152
                    % Var explained: 56.42
set.seed(32435)
forest_pred1 <- predict(forest1, newdata = data2024_noheight)
forest_pred1 * 538
       1        2        3        4        5        6        7        8 
227.0768 229.9066 290.7208 227.5034 281.8953 306.2310 184.2865 264.3723 
       9 
258.2720


random forest (5 variables boostrap sampled):

set.seed(32435)
forest1 <- randomForest(Pct_incumb ~ .,
                        ntree = 501,
                        nodesize = 1,
                        data = dta_noheight,
                        na.action = na.omit,
                        mtry = 5,
                        importance = TRUE)
forest1

Call:
 randomForest(formula = Pct_incumb ~ ., data = dta_noheight, ntree = 501,      nodesize = 1, mtry = 5, importance = TRUE, na.action = na.omit) 
               Type of random forest: regression
                     Number of trees: 501
No. of variables tried at each split: 5

          Mean of squared residuals: 0.04000085
                    % Var explained: 42.15
set.seed(32435)
forest_pred1 <- predict(forest1, newdata = data2024_noheight)
forest_pred1 * 538
       1        2        3        4        5        6        7        8 
266.9741 269.2456 297.0022 250.5545 264.2572 317.4231 188.6188 285.1010 
       9 
272.9281


Win/Lose (R Code)

With Height

clean data

win <- read_csv("win.csv")
win2024 <- win[1:9,]
win2024 <- win2024[,-2]
win <- win[-c(1:3),] # get rid of first 3 row
win$win <- as.factor(win$win)


bagging

set.seed(32435)
bagging_win <- randomForest(win ~ .,
                        ntree = 501,
                        nodesize = 1,
                        data = win,
                        na.action = na.omit,
                        mtry = 28,
                        importance = TRUE)
bagging_win

Call:
 randomForest(formula = win ~ ., data = win, ntree = 501, nodesize = 1,      mtry = 28, importance = TRUE, na.action = na.omit) 
               Type of random forest: classification
                     Number of trees: 501
No. of variables tried at each split: 28

        OOB estimate of  error rate: 27.27%
Confusion matrix:
  0 1 class.error
0 8 2   0.2000000
1 4 8   0.3333333
#prediction
set.seed(32435)
bagging_winpred <- predict(bagging_win, newdata = win2024, type = "prob")
bagging_winpred
          0          1
1 0.6866267 0.31337325
2 0.6846307 0.31536926
3 0.6227545 0.37724551
4 0.8642715 0.13572854
5 0.7844311 0.21556886
6 0.1836327 0.81636727
7 0.9900200 0.00998004
8 0.1876248 0.81237525
9 0.8722555 0.12774451
attr(,"class")
[1] "matrix" "array"  "votes"


Random Forest (5 vairables boostrap sampled):

bagging_win <- randomForest(win ~ .,
                        ntree = 501,
                        nodesize = 1,
                        data = win,
                        na.action = na.omit,
                        mtry = 5,
                        importance = TRUE)
bagging_win

Call:
 randomForest(formula = win ~ ., data = win, ntree = 501, nodesize = 1,      mtry = 5, importance = TRUE, na.action = na.omit) 
               Type of random forest: classification
                     Number of trees: 501
No. of variables tried at each split: 5

        OOB estimate of  error rate: 31.82%
Confusion matrix:
  0 1 class.error
0 8 2   0.2000000
1 5 7   0.4166667
set.seed(32435)
bagging_winpred <- predict(bagging_win, newdata = win2024, type = "prob")
bagging_winpred
          0          1
1 0.5888224 0.41117764
2 0.5868263 0.41317365
3 0.5489022 0.45109780
4 0.8423154 0.15768463
5 0.8003992 0.19960080
6 0.1956088 0.80439122
7 0.9600798 0.03992016
8 0.2195609 0.78043912
9 0.8323353 0.16766467
attr(,"class")
[1] "matrix" "array"  "votes"


naive bayes

library(e1071)
bayes <- naiveBayes(win ~ ., data = win)
set.seed(32435)
bayes_winpred <- predict(bayes, newdata = win2024, type = "raw")

bayes_winpred
                 0            1
 [1,] 0.9995677419 4.322581e-04
 [2,] 0.9994574316 5.425684e-04
 [3,] 0.9992597549 7.402451e-04
 [4,] 0.9999948160 5.184010e-06
 [5,] 0.9999765940 2.340603e-05
 [6,] 0.0001471148 9.998529e-01
 [7,] 1.0000000000 1.548431e-13
 [8,] 0.1160488759 8.839511e-01
 [9,] 0.9941196876 5.880312e-03


Without Height

win_noheight <- win %>%
  select(-height)
win2024_noheight <- win2024 %>%
  select(-height)


Bagging:

set.seed(32435)
bagging_win1 <- randomForest(win ~ .,
                        ntree = 501,
                        nodesize = 1,
                        data = win_noheight,
                        na.action = na.omit,
                        mtry = 27,
                        importance = TRUE)
bagging_win1

Call:
 randomForest(formula = win ~ ., data = win_noheight, ntree = 501,      nodesize = 1, mtry = 27, importance = TRUE, na.action = na.omit) 
               Type of random forest: classification
                     Number of trees: 501
No. of variables tried at each split: 27

        OOB estimate of  error rate: 22.73%
Confusion matrix:
  0 1 class.error
0 8 2        0.20
1 3 9        0.25
set.seed(32435)
bagging_winpred1 <- predict(bagging_win1, newdata = win2024_noheight, type = "prob")
bagging_winpred1
          0          1
1 0.6506986 0.34930140
2 0.6487026 0.35129741
3 0.5748503 0.42514970
4 0.8722555 0.12774451
5 0.7684631 0.23153693
6 0.1756487 0.82435130
7 0.9680639 0.03193613
8 0.2055888 0.79441118
9 0.8403194 0.15968064
attr(,"class")
[1] "matrix" "array"  "votes"


Random Forest (5 Variables bootstrapped):

set.seed(32435)
bagging_win1 <- randomForest(win ~ .,
                        ntree = 501,
                        nodesize = 1,
                        data = win_noheight,
                        na.action = na.omit,
                        mtry = 5,
                        importance = TRUE)
bagging_win1

Call:
 randomForest(formula = win ~ ., data = win_noheight, ntree = 501,      nodesize = 1, mtry = 5, importance = TRUE, na.action = na.omit) 
               Type of random forest: classification
                     Number of trees: 501
No. of variables tried at each split: 5

        OOB estimate of  error rate: 27.27%
Confusion matrix:
  0  1 class.error
0 6  4   0.4000000
1 2 10   0.1666667
set.seed(32435)
bagging_winpred1 <- predict(bagging_win1, newdata = win2024_noheight, type = "prob")
bagging_winpred1
          0          1
1 0.5489022 0.45109780
2 0.5489022 0.45109780
3 0.5329341 0.46706587
4 0.8243513 0.17564870
5 0.8283433 0.17165669
6 0.1377246 0.86227545
7 0.9640719 0.03592814
8 0.1696607 0.83033932
9 0.8103792 0.18962076
attr(,"class")
[1] "matrix" "array"  "votes"


Naive Bayes:

set.seed(32435)
bayes1 <- naiveBayes(win ~ ., data = win_noheight)
bayes_winpred1 <- predict(bayes1, newdata = win2024_noheight, type = "raw")

set.seed(32435)
bayes_winpred1
                 0            1
 [1,] 0.9397623361 6.023766e-02
 [2,] 0.9255270741 7.447293e-02
 [3,] 0.9010603924 9.893961e-02
 [4,] 0.9999976463 2.353692e-06
 [5,] 0.9976060912 2.393909e-03
 [6,] 0.0001890752 9.998109e-01
 [7,] 1.0000000000 6.021154e-13
 [8,] 0.0326591074 9.673409e-01
 [9,] 0.9966782550 3.321745e-03